A Hitchhiker's Guide to the FFT
V. Matlab fft function
V.1 What fft actually does
For a given vector x of size N, the Matlab command fft(x) returns the \(N\)-DFT of x. Note that in practice, in order to optimise the speed of execution, one should choose N as a power of 2. Hence fft is just a fast way to compute the Discrete Fourier Transform. We know that the Fourier transform of a real, even function is real. Hence when taking the fft of an even vector, we should obtain a real value. But what is an even vector? This is indeed an important question since the index of a vector in Matlab starts at 1, there is no such thing as a negative index, and we cannot create the vector plotted on Figure 3. The first thing to do is to sample the physical signal in an appropriate way.
V.2 Do not repeat the last point
The fft algorithm assumes that the first and last point of your signal are the same. Hence when sampling the signal, it would be redundant to include the last point. Worst than that, it would lead to WRONG results. The following two figures illustrate the problem, by considering two different ways of sampling the same signal with N points. The ''bad'' sample is obtained as follows
eta_sampled_bad=linspace(-1,1,N);
while the ''good'' sample is obtained by
eta_sampled=linspace(-1,1,N+1);
eta_sampled_good=eta_sampled(1:end-1);
Now, in the following code, replace eta_sampled by eta_sampled_bad or eta_sampled_good to obtain the plots of the sampled signals of Figure 8 or Figure 9.
x=max(1-abs(eta_sampled),0);
plot(eta,fc,'b');
hold on
stem(eta_sampled,x,'r');
hold off
axis([-3 3 -0.5 1.5]);
xlabel('\eta'); ylabel('f(\eta)');
The plots of the fft is obtained by running the following piece of code
k_fft=0:(N-1);
X_fft=fft(x);
stem(k_fft,real(X_fft),'r');
hold on
stem(k_fft,imag(X_fft),'b');
hold off
legend('real part','imaginary part'); xlabel('k');
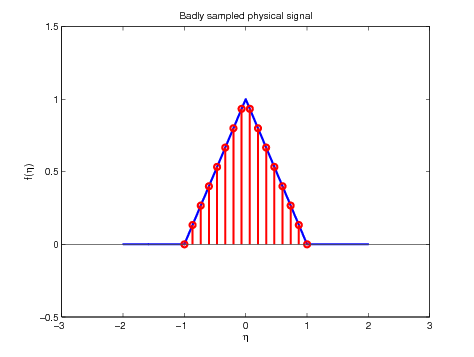
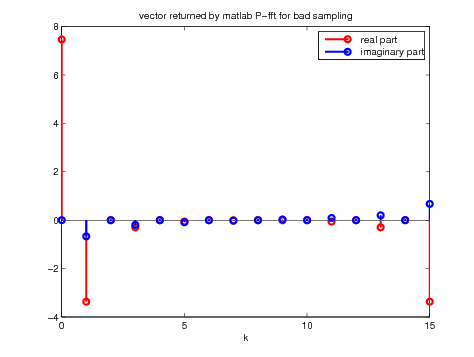
Figure 8. ''Bad'' sample (left) and its fft (right) for \(P = N =
16\)
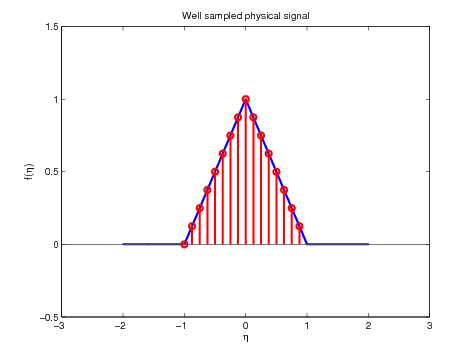
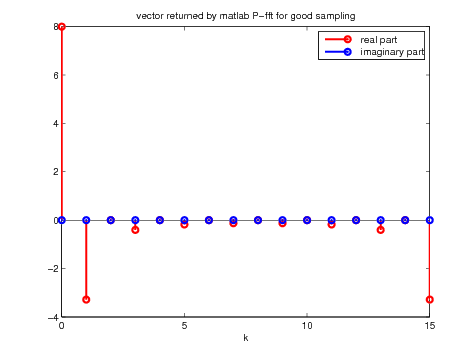
Figure 9. ''Good'' sample (left) and its fft (right) for \(P = N =
16\)
As one can see, the result returned by the fft for the ''bad'' sampling has all the chances to be wrong. Indeed, despite the signal being even in an intuitive way, the fft is far from even being real! The well sampled signal is closer to what we expected since the result returned by the fft is real. However, from what the fft claims to do (i.e. returning the P-DFT), there seems to be a problem with the sign of the real part of our results when comparing the right plot of Figure 9 with the left plot of Figure 5. Hence we need to do something else before obtaining the expected result.
V.3 Shift the signal
Another thing to do before taking the fft is to shift the signal appropriately. Indeed, if you imagine that you repeat your signal periodically in both directions by including negative indexes. Then restrain your signal to $n \in [- N / 2, N / 2]$. It doesn't look like the original signal. So the good thing to do is to shift the signal as illustrated by the following figure and can be achieved by typing
x=max(1-abs(eta_sampled_good),0);
x_shift=circshift(x,[0 -N/2]);
plot(eta,fc,'b');
hold on
stem(eta_sampled_good,x_shift,'r');
hold off
xlabel('eta'); axis([-3 3 -0.5 1.5]);
legend('continuous signal','shifted signal');
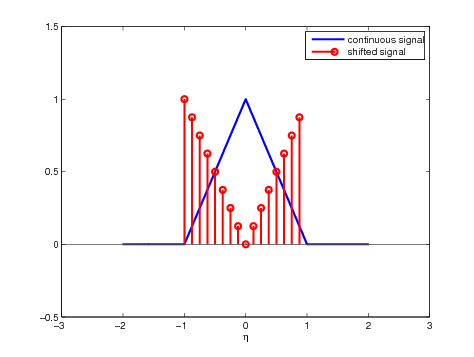
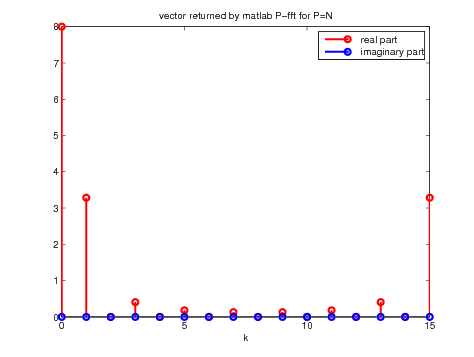
Figure 10. Illustration of the vector shift required before taking the fft
As one can see, the right part of Figure 10 is identical to the left part of Figure 5. Victory. At this stage, with learned to create the fft of size \(N\) of a sampled signal of size \(N\). But as seen in Section III, it should be possible to create the fft of size \(P \neq N\). This is achieved by the technique of zero-padding.
V.4 Zero-padding
Roughly speaking, the zero-padding consists in adding some zeros to the original signal before taking the fft in order to have a result with a better resolution. But again, one should be careful on how to proceed. The first step is to add some zeros to the well sampled signal as can be seen on the following figure. This can be obtained by typing the following code
multi=2; P=multi*N;
xP=x; xP(P)=0;
stem(xP,'r'); xlabel('n');
title('sampled signal with added zeros');
Then the signal should be shifted by typing
xP_shift=circshift(xP,[0 -N/2]);
stem(xP_shift,'r'); xlabel('n');
title('shift of the signal with added zeros');
Note that the zeros should be added before shifting the signal.
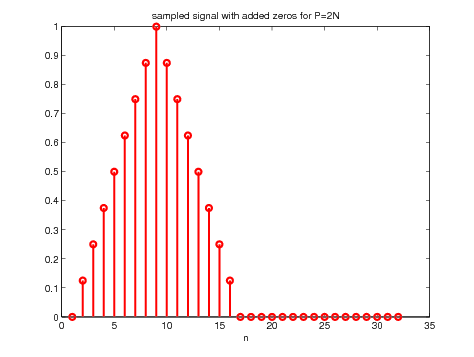
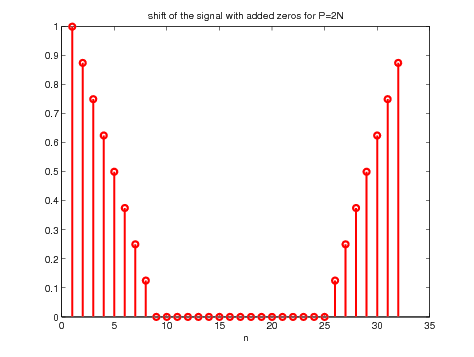
Figure 11. Illustration of the signal preparation for zero padding with N
extra points
The fft is then computed as before:
k_fft=0:(P-1);
X_fft=fft(xP_shift);
stem(k_fft,real(X_fft),'r');
hold on
stem(k_fft,imag(X_fft),'b');
hold off
legend('real part','imaginary part');
xlabel('k');
title('vector returned by matlab P-fft for P=2N');
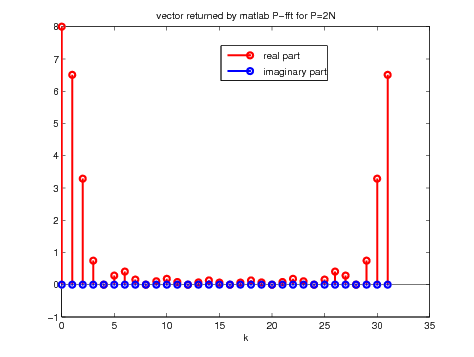
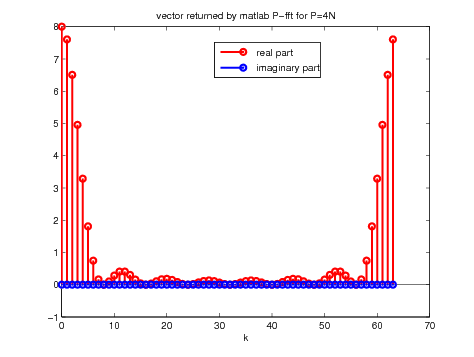
Figure 12. Result of taking the fft of the zero padded signal with \(N\) (left)
and \(3 N\)(right) extra points
Note that on Figure 12, we recover exactly the analytic results of Figure 5 and Figure 6.
