Canonical Scattering Problems
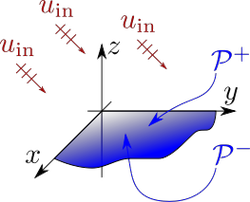 Diagrammatic view of an incident plane wave on a quarter-plane
Diagrammatic view of an incident plane wave on a quarter-plane
Brief overview
There is a long history of mathematicians working on canonical diffraction (or scattering) problems. The mathematical theory of diffraction probably started with the work of Sommerfeld at the end of the 19th century and his famous solution to the diffraction of acoustic waves by a solid half-plane. Since, some very ingenious mathematical methods have been developed to tackle such problems. One of the most famous being the Wiener-Hopf technique.
However, despite tremendous efforts in this field, some canonical problems remain open, in the sense that no clear analytical solution is available for them.
One of this problem is the quarter-plane problem, the problem of diffraction of acoustic waves by a solid quarter-plane. Thus far, it has not been possible to apply classical methods such as the Wiener-Hopf method successfully in that case, and hence some new mathematical methods need to be developed in order to tackle this problem.
There is a long history of mathematicians working on canonical diffraction (or scattering) problems. The mathematical theory of diffraction probably started with the work of Sommerfeld at the end of the 19th century and his famous solution to the diffraction of acoustic waves by a solid half-plane. Since, some very ingenious mathematical methods have been developed to tackle such problems. One of the most famous being the Wiener-Hopf technique.
However, despite tremendous efforts in this field, some canonical problems remain open, in the sense that no clear analytical solution is available for them.
One of this problem is the quarter-plane problem, the problem of diffraction of acoustic waves by a solid quarter-plane. Thus far, it has not been possible to apply classical methods such as the Wiener-Hopf method successfully in that case, and hence some new mathematical methods need to be developed in order to tackle this problem.
 The countra-rotating open-rotor engine, particularly noisy, can be linked to the quarter-plane problem.
The countra-rotating open-rotor engine, particularly noisy, can be linked to the quarter-plane problem.
This makes it very interesting as it implies that many different types of mathematics can be used and it makes the subject intrinsically multidisciplinary.
However, many industrial problems can also be linked to the theory of diffraction, for example:
However, many industrial problems can also be linked to the theory of diffraction, for example:
- the noise generated by a jet engine (acoustic waves) for the scalar Helmholtz equation
- radar detection (electro-magnetic waves) for the vectorial Helmholtz equation
- defect detection in materials (elastic waves)
|
Scalar Helmholtz equation $$\begin{aligned} \Delta u +k^2 u = 0 \end{aligned}$$ |
Vectorial Helmholtz equation $$\begin{aligned} \Delta \boldsymbol{E} +k^2 \boldsymbol{E} = 0 \end{aligned}$$ |
Bi-harmonic (flexural wave) equation $$\begin{aligned} \left(\Delta -\beta^2\right)\left(\Delta +\beta^2\right)w = 0 \end{aligned}$$ |
- R. C. Assier and N. Peake. On the diffraction of acoustic waves by a quarter-plane. Wave Motion, 49(1):64-82, 2012.
- R. C. Assier and N. Peake. Precise description of the different far fields encountered in the problem of diffraction of acoustic waves by a quarter-plane. IMA J. Appl. Math., 77(5):605-625, 2012.
